Page 308 - AI Computer 10

are commonly used to create these types of effects by changing the pixel values evenly throughout the image.
Let us understand the theory of convolution through the following definitions.
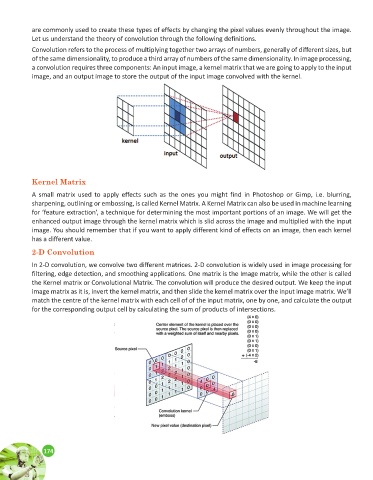
Convolution refers to the process of multiplying together two arrays of numbers, generally of different sizes, but
of the same dimensionality, to produce a third array of numbers of the same dimensionality. In image processing,
a convolution requires three components: An input image, a kernel matrix that we are going to apply to the input
image, and an output image to store the output of the input image convolved with the kernel.

Kernel Matrix

A small matrix used to apply effects such as the ones you might find in Photoshop or Gimp, i.e. blurring,
sharpening, outlining or embossing, is called Kernel Matrix. A Kernel Matrix can also be used in machine learning
for ‘feature extraction’, a technique for determining the most important portions of an image. We will get the
enhanced output image through the kernel matrix which is slid across the image and multiplied with the input
image. You should remember that if you want to apply different kind of effects on an image, then each kernel
has a different value.

2-D Convolution

In 2-D convolution, we convolve two different matrices. 2-D convolution is widely used in image processing for
filtering, edge detection, and smoothing applications. One matrix is the Image matrix, while the other is called
the Kernel matrix or Convolutional Matrix. The convolution will produce the desired output. We keep the input
image matrix as it is, invert the kernel matrix, and then slide the kernel matrix over the input image matrix. We’ll
match the centre of the kernel matrix with each cell of of the input matrix, one by one, and calculate the output
for the corresponding output cell by calculating the sum of products of intersections.

174
174